Limit calculator helps you find the limit of a function with respect to a variable. This limits calculator is an online tool that assists you in calculating the value of a function when an input approaches some specific value.

Limit calculator with steps shows the step-by-step solution of limits along with a plot and series expansion. It employs all limit rules such as sum , product, quotient, and L'hopital's rule to calculate the exact value.
You can evaluate limits with respect to \(\text\) and \(w\) using this limits calculator.
That’s not it. By using this tool, you can also find,
To evaluate the limit using this limit solver, follow the below steps.
The limit of a function is the value that f(x) gets closer to as x approaches some number. Limits can be used to define the derivatives , integrals , and continuity by finding the limit of a given function. It is written as:
If f is a real-valued function and a is a real number, then the above expression is read as,
the limit of f of x as x approaches a equals L.
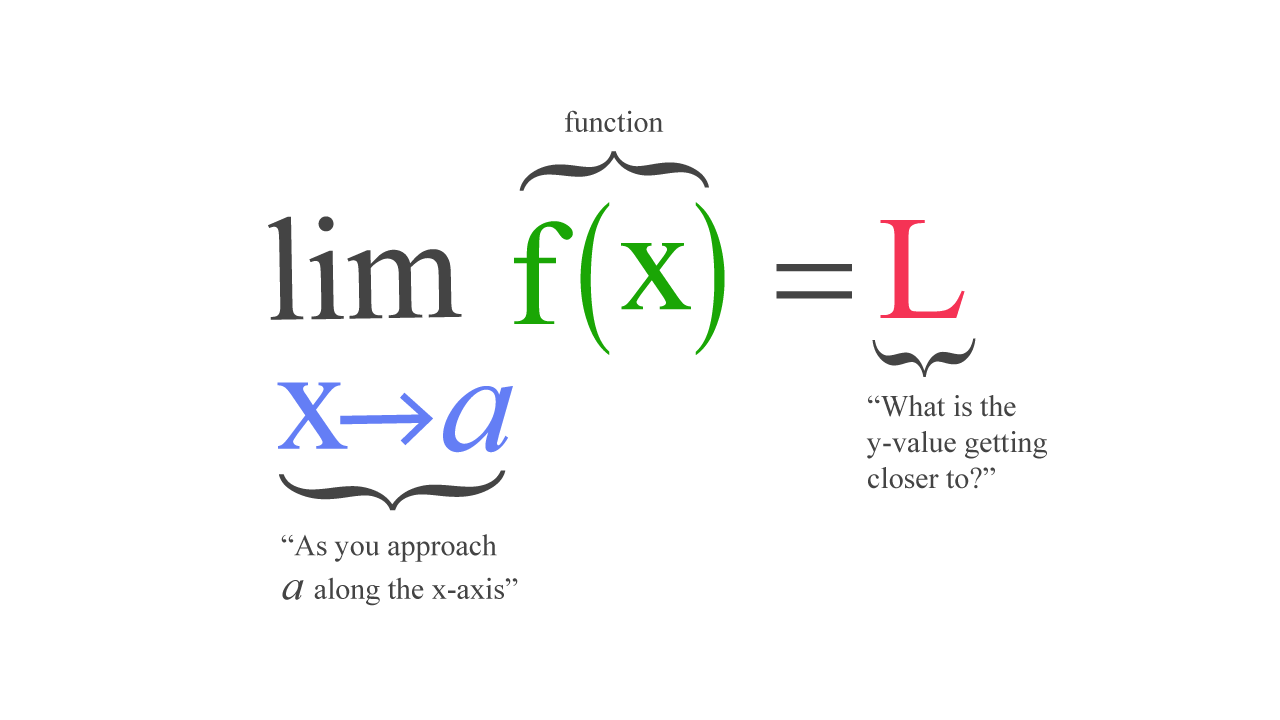
Limits can be applied as numbers, constant values (π, G, k), infinity, etc. Let’s go through a few examples to learn how to calculate limits.
Example - Right-hand LimitSolution:
A right-hand limit means the limit of a function as it approaches from the right-hand side.
Step 1: Apply the limit x➜2 to the above function. Put the limit value in place of x.
\(\lim \:_\frac<\left(x^2+2\right)><\left(x-1\right)>\)
Step 2: Solve the equation to reach a result.
Step 3: Write the expression with its answer.
Solution:
A left-hand limit means the limit of a function as it approaches from the left-hand side.
Step 1: Place the limit value in the function.
Step 2: Solve the equation further.
Step 3: Write down the function as written below.
\( \lim _\left(cos^3\left(x\right)\cdot sin\left(x\right)\right) \)
Solution:
A two-sided limit exists if the limit coming from both directions (positive and negative) is the same. It is the same as a limit.
Step 1: Substitute the value of the limit in the function.
\(\lim _\left(cos^3\left(x\right)\cdot sin\left(x\right)\right)\)
Step 2: Simplify the equation as we did in previous examples.
\( \lim _\left(cos^3\left(x\right)\cdot sin\left(x\right)\right) \)
Step 3: The above equation can be considered as the final answer. However, if you want to solve it further, solve the trigonometric values in the equation.
\(\lim \:\:_\left(cos^3\left(x\right)\cdot \:\:sin\left(x\right)\right)\)
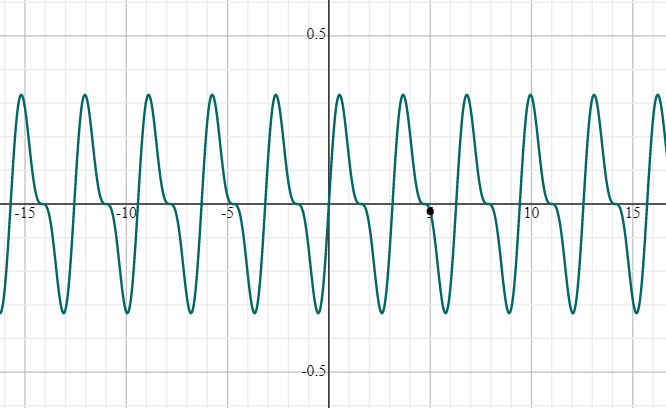
Does sin x have a limit?
Sin x has no limit. It is because, as x approaches infinity, the y-value oscillates between 1 and −1.
What is the limit of e to infinity?
The limit of e to the infinity (∞) is e.
What is the limit as e^x approaches 0?
The limit as e^x approaches 0 is 1.
What is the limit as x approaches the infinity of ln(x)?
The limit as x approaches the infinity of ln(x) is +∞. The limit of this natural log can be proved by reductio ad absurdum.